

The moment of inertia is generally smaller for a body with a more compact and symmetrical shape and larger for a body with a more elongated or irregular shape. The moment of inertia of a body depends on several factors, including: So, the unit of moment of inertia is, kg-m² or kg-mm² or kg-cm² and Its dimension is ML².įactors on which Moment of Inertia Depends We can use the above expression for determining the moment of inertia of some of the common bulk objects of interest like rods, rings, discs, spheres, etc. We get the moment of inertia of the entire bulk object by integrating the above expression. The moment of inertia of this point mass can now be written as, To find the moment of inertia of a uniformly distributed mass we have to consider an infinitesimally small mass (dm) as a point mass and take its position (r) with respect to an axis. It depends not only on the mass of the body but also on the way the mass is distributed around the axis of rotation. In general, mass is an invariable quantity of matter (except for motion comparable to that of light).īut, the moment of inertia of a body is not an invariable quantity. In translational motion, mass is a measure of inertia in the same way, for rotational motion, a moment of inertia is a measure of rotational inertia. R = Distance from the axis of the rotation. For point mass m, at a distance r, from the fixed axis, the moment of inertia is given as, mr².

This quantity is called the moment of inertia (I) of the bulk object. In the expressions for torque and angular momentum for rigid bodies (which are considered bulk objects), we have come across the term Σmr². In general, objects with more mass concentrated towards their center of mass have a smaller moment of inertia than objects with mass distributed more evenly. The moment of inertia of an object depends on the object's shape, size, and mass distribution.įor example, a solid cylinder has a different moment of inertia than a hollow cylinder of the same size and mass. The greater the moment of inertia, the more difficult it is to change the object's rotational speed or direction.

It is defined as the sum of the products of the mass of each particle in an object and the square of its distance from the object's axis of rotation. Moment of inertia, also known as rotational inertia, mass moment of inertia, angular mass, and second moment of mass is a measure of an object's resistance to change in its rotational motion. We have also discussed the polar moment of inertia, area moment of inertia, first moment of area in our previous article here we will learn only about the moment of inertia.
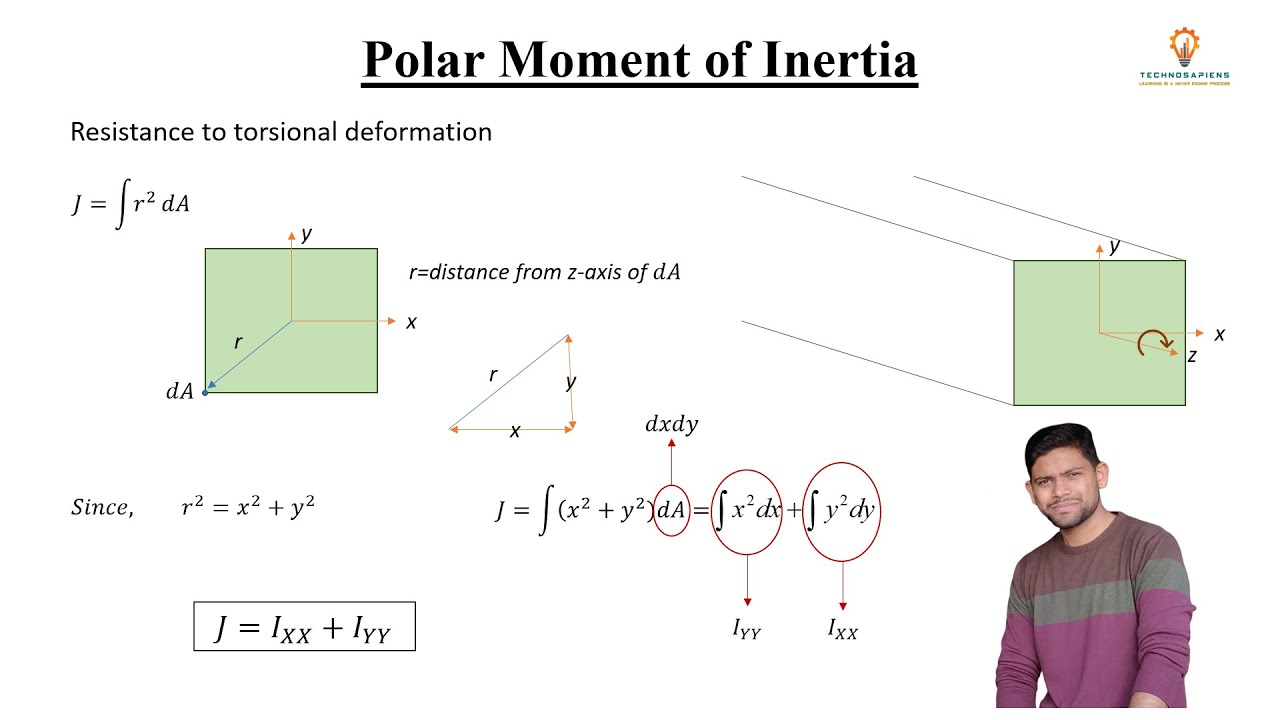
It is also used to determine the stability of an object when it is rotating, as well as to predict the motion of objects under the influence of external forces or torques. It is used to calculate the torque required to rotate an object about a given axis, as well as the angular acceleration of the object under the influence of a given torque. Moment of inertia concerned with the dynamics. In physics and mechanics, the moment of inertia plays an important role in the analysis of the rotational motion of objects. In this article, you will learn a complete overview of the moment of inertia such as its definition, formula of different sections, units, depending factors, calculation, and many more.


 0 kommentar(er)
0 kommentar(er)
